Minimal Spanning Tree

What is a Spanning Tree?

Given an undirected and connected graph $G=(V,E)$, a spanning tree of the graph $G$ is a tree that spans $G$ (that is, it includes every vertex of $G$) and is a subgraph of $G$ (every edge in the tree belongs to $G$)

What is a Minimum Spanning Tree?

The cost of the spanning tree is the sum of the weights of all the edges in the tree. There can be many spanning trees. Minimum spanning tree is the spanning tree where the cost is minimum among all the spanning trees. There also can be many minimum spanning trees.

Minimum spanning tree has direct application in the design of networks. It is used in algorithms approximating the travelling salesman problem, multi-terminal minimum cut problem and minimum-cost weighted perfect matching. Other practical applications are:

1. Cluster Analysis
2. Handwriting recognition
3. Image segmentation

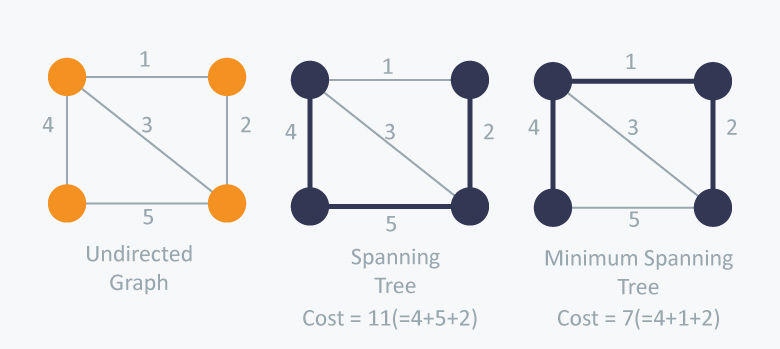
Reference: https://www.hackerearth.com/practice/algorithms/graphs/minimum-spanning-tree/tutorial/