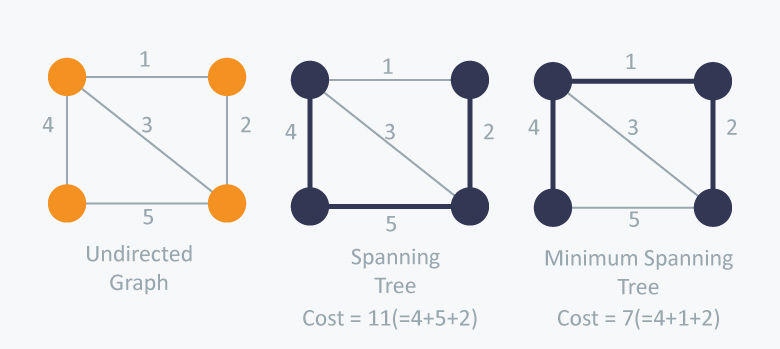
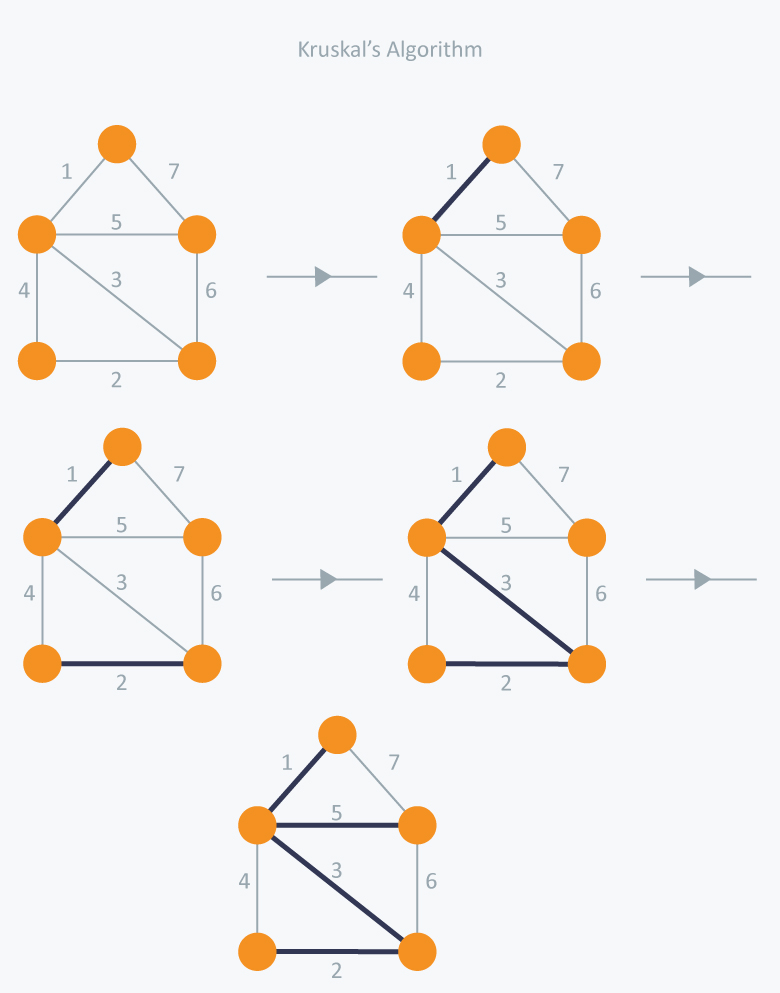
Task:
In this task you have to implement the kruskal's algorithm for minimal spanning tree. You can use the class "MyGraph" which you have created in your previous lab.
Helping Materiel:
Kruskal’s Algorithm
Kruskal’s Algorithm builds the spanning tree by adding edges one by one into a growing spanning tree. Kruskal's algorithm follows greedy approach as in each iteration it finds an edge which has least weight and add it to the growing spanning tree.
Algorithm Steps:
- Sort the graph edges with respect to their weights.
- Start adding edges to the MST from the edge with the smallest weight until the edge of the largest weight.
- Only add edges which doesn't form a cycle , edges which connect only disconnected components.
So now the question is how to check if 2 vertices are connected or not ?
This could be done using DFS which starts from the first vertex, then check if the second vertex is visited or not. But DFS will make time complexity large as it has an order of O(V+E) where V is the number of vertices, E is the number of edges. So the best solution is "Disjoint Sets":
Disjoint sets are sets whose intersection is the empty set so it means that they don't have any element in common.
Consider following example:
In Kruskal’s algorithm, at each iteration we will select the edge with the lowest weight. So, we will start with the lowest weighted edge first i.e., the edges with weight 1. After that we will select the second lowest weighted edge i.e., edge with weight 2. Notice these two edges are totally disjoint. Now, the next edge will be the third lowest weighted edge i.e., edge with weight 3, which connects the two disjoint pieces of the graph. Now, we are not allowed to pick the edge with weight 4, that will create a cycle and we can’t have any cycles. So we will select the fifth lowest weighted edge i.e., edge with weight 5. Now the other two edges will create cycles so we will ignore them. In the end, we end up with a minimum spanning tree with total cost 11 ( = 1 + 2 + 3 + 5).
Implementation:
#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
using namespace std;
const int MAX = 1e4 + 5;
int id[MAX], nodes, edges;
pair <long long, pair<int, int> > p[MAX];
void initialize()
{
for(int i = 0;i < MAX;++i)
id[i] = i;
}
int root(int x)
{
while(id[x] != x)
{
id[x] = id[id[x]];
x = id[x];
}
return x;
}
void union1(int x, int y)
{
int p = root(x);
int q = root(y);
id[p] = id[q];
}
long long kruskal(pair<long long, pair<int, int> > p[])
{
int x, y;
long long cost, minimumCost = 0;
for(int i = 0;i < edges;++i)
{
// Selecting edges one by one in increasing order from the beginning
x = p[i].second.first;
y = p[i].second.second;
cost = p[i].first;
// Check if the selected edge is creating a cycle or not
if(root(x) != root(y))
{
minimumCost += cost;
union1(x, y);
}
}
return minimumCost;
}
int main()
{
int x, y;
long long weight, cost, minimumCost;
initialize();
cin >> nodes >> edges;
for(int i = 0;i < edges;++i)
{
cin >> x >> y >> weight;
p[i] = make_pair(weight, make_pair(x, y));
}
// Sort the edges in the ascending order
sort(p, p + edges);
minimumCost = kruskal(p);
cout << minimumCost << endl;
return 0;
}
Time Complexity:
In Kruskal’s algorithm, most time consuming operation is sorting because the total complexity of the Disjoint-Set operations will be O(ElogV), which is the overall Time Complexity of the algorithm.
Reference: This content is taken from https://www.hackerearth.com/practice/algorithms/graphs/minimum-spanning-tree/tutorial/