Graph Data Structure

A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.

Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −

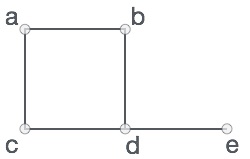
In the above graph,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Graph Data Structure

Mathematical graphs can be represented in data structure. We can represent a graph using an array of vertices and a two-dimensional array of edges. Before we proceed further, let's familiarize ourselves with some important terms −

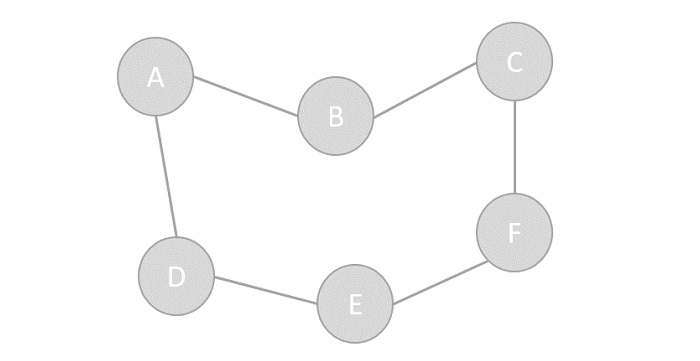
• Vertex − Each node of the graph is represented as a vertex. In the following example, the labeled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
• Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
• Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
• Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.

Basic Operations

Following are basic primary operations of a Graph −

• Add Vertex − Adds a vertex to the graph.
• Add Edge − Adds an edge between the two vertices of the graph.
• Display Vertex − Displays a vertex of the graph.

Depth First Traversal

Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

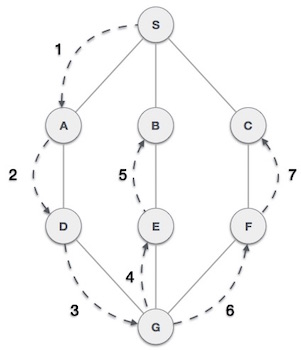
As in the example given above, DFS algorithm traverses from A to B to C to D first then to E, then to F and lastly to G. It employs the following rules.

• Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
• Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
• Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.

Step	Traversal	Description
1.		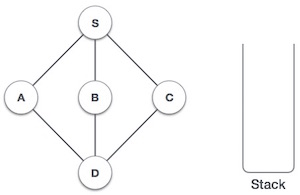Initialize the stack.
2.		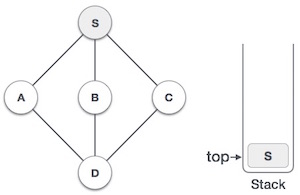Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order.
3.		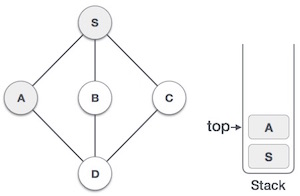Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only.
4.		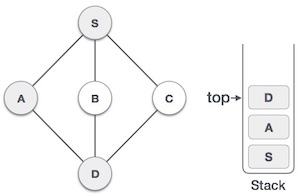Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order.
5.		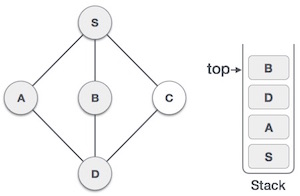We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack.
6.		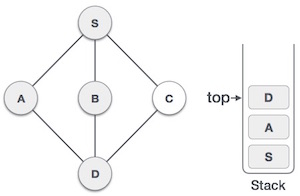We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack.
7.		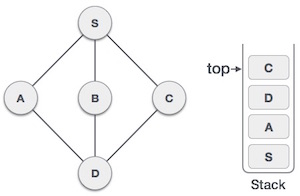Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack.

As C does not have any unvisited adjacent node so we keep popping the stack until we find a node that has an unvisited adjacent node. In this case, there's none and we keep popping until the stack is empty.

Breadth First Traversal

Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

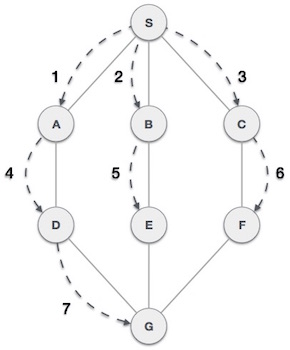
As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules.

• Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
• Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
• Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.

Step	Traversal	Description
1.		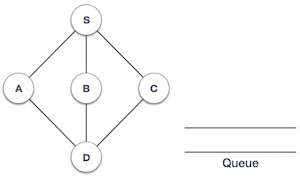Initialize the queue.
2.		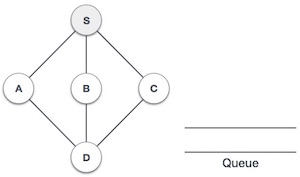We start from visiting S (starting node), and mark it as visited.
3.		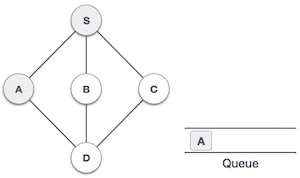We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it.
4.		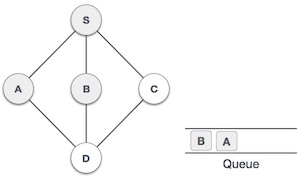Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it.
5.		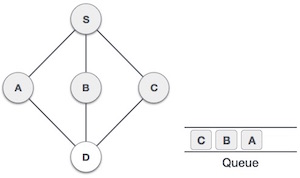Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it.
6.		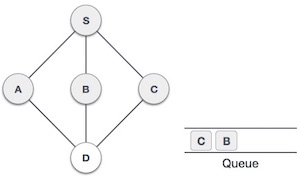Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A.
7.		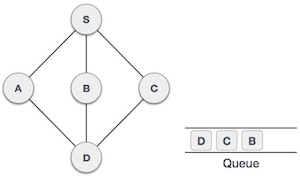From A we have D as unvisited adjacent node. We mark it as visited and enqueue it.

At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.