Graph Data Structure

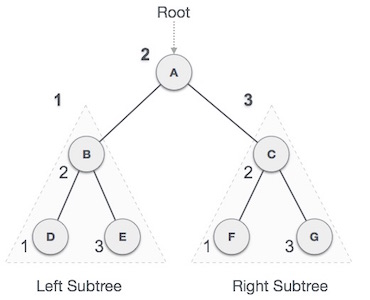
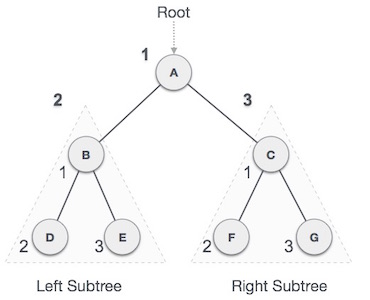
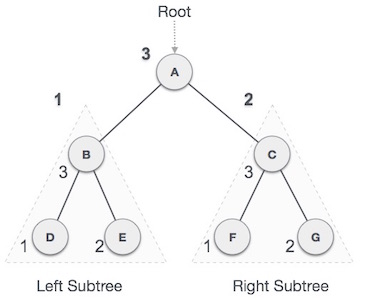
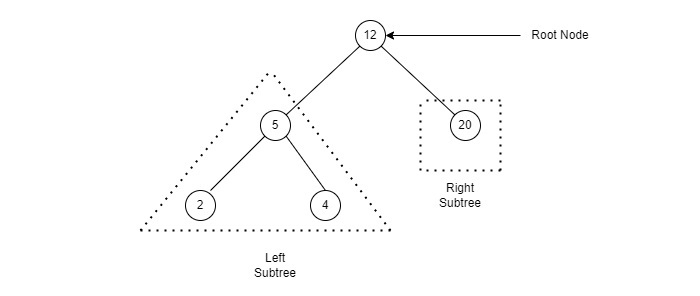
A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.

Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −

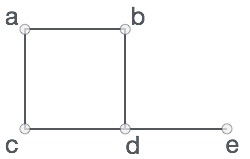
In the above graph,

V = {a, b, c, d, e}

E = {ab, ac, bd, cd, de}

Graph Data Structure

Mathematical graphs can be represented in data structure. We can represent a graph using an array of vertices and a two-dimensional array of edges. Before we proceed further, let's familiarize ourselves with some important terms −

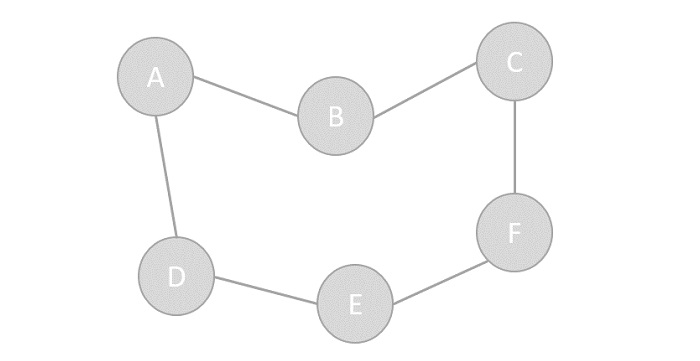
• Vertex − Each node of the graph is represented as a vertex. In the following example, the labeled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
• Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
• Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
• Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.

Basic Operations

Following are basic primary operations of a Graph −

• Add Vertex − Adds a vertex to the graph.
• Add Edge − Adds an edge between the two vertices of the graph.
• Display Vertex − Displays a vertex of the graph.

Depth First Traversal

Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

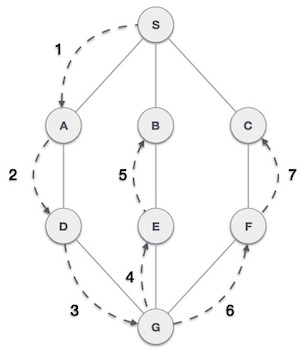
As in the example given above, DFS algorithm traverses from A to B to C to D first then to E, then to F and lastly to G. It employs the following rules.

• Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
• Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
• Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.

Step	Traversal	Description
1.		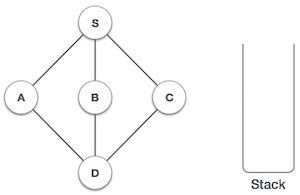Initialize the stack.
2.		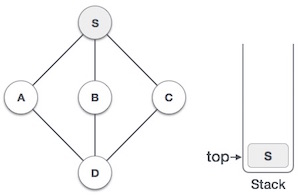Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order.
3.		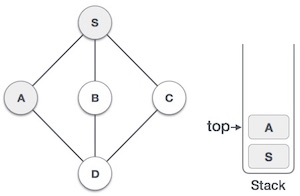Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only.
4.		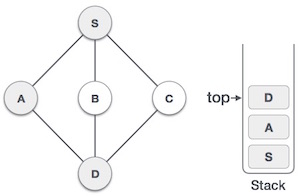Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order.
5.		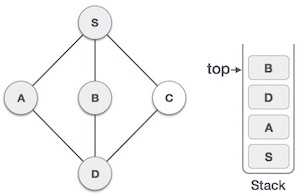We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack.
6.		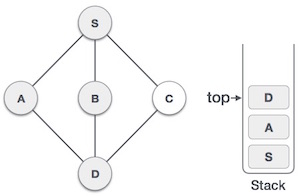We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack.
7.		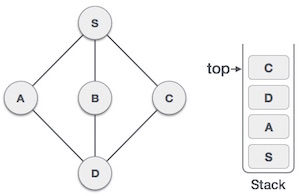Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack.

As C does not have any unvisited adjacent node so we keep popping the stack until we find a node that has an unvisited adjacent node. In this case, there's none and we keep popping until the stack is empty.

Breadth First Traversal

Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

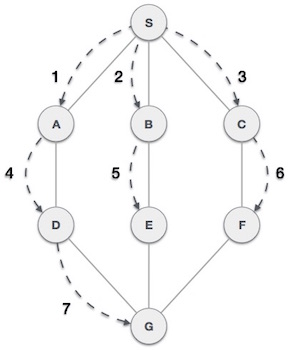
As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules.

• Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
• Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
• Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.

Step	Traversal	Description
1.		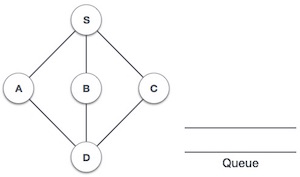Initialize the queue.
2.		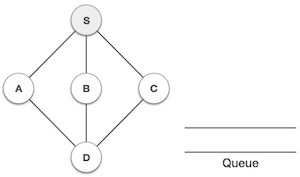We start from visiting S (starting node), and mark it as visited.
3.		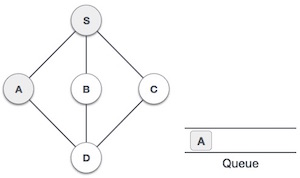We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it.
4.		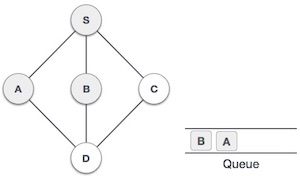Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it.
5.		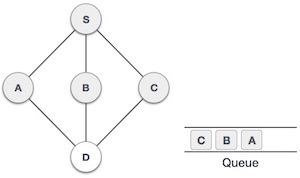Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it.
6.		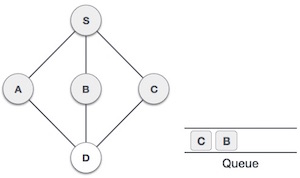Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A.
7.		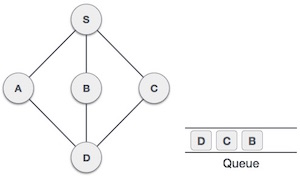From A we have D as unvisited adjacent node. We mark it as visited and enqueue it.

At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.

DSA Lab 8: Graph Data Structure, DFS, BFS

Task:

Implement the class "MyGraph" as discussed in class. For this you have to write a class "MyNode" and create whole graph class using this node class. Your class contains all necessary functions with the additions of these functions:

• display_DFS()        //this will display the whole tree in depth first manner
• display_BFS()        //this will display the whole tree in breath first manner
• MyGraph()        //this is the constructor, it will create graph as shown in following example

Helping Materiel:

Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.

As in the example given above, DFS algorithm traverses from A to B to C to D first then to E, then to F and lastly to G. It employs the following rules.

• Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
• Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
• Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.

Step	Traversal	Description
1.		Initialize the stack.
2.		Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order.
3.		Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only.
4.		Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order.
5.		We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack.
6.		We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack.
7.		Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack.

As C does not have any unvisited adjacent node so we keep popping the stack until we find a node that has an unvisited adjacent node. In this case, there's none and we keep popping until the stack is empty.

Tree Traversal

Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −

• In-order Traversal
• Pre-order Traversal
• Post-order Traversal

Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.

If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.

We start from A, and following in-order traversal, we move to its left subtree B. B is also traversed in-order. The process goes on until all the nodes are visited. The output of inorder traversal of this tree will be −

D → B → E → A → F → C → G

Algorithm

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.

Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be −

A → B → D → E → C → F → G

Algorithm

Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.

Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

We start from A, and following pre-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be −

D → E → B → F → G → C → A

Algorithm

Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.

Binary Search Tree | Search and Insertion

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −

• The left sub-tree of a node has a key less than or equal to its parent node's key.
• The right sub-tree of a node has a key greater than to its parent node's key.

Thus, BST divides all its sub-trees into two segments; the left sub-tree and the right sub-tree and can be defined as −

left_subtree (keys)  ≤  node (key)  ≤  right_subtree (keys)

Representation

BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has a key and an associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved.

Following is a pictorial representation of BST −

We observe that the root node key (27) has all less-valued keys on the left sub-tree and the higher valued keys on the right sub-tree.

Basic Operations

Following are the basic operations of a tree −

• Search − Searches an element in a tree.
• Insert − Inserts an element in a tree.
• Pre-order Traversal − Traverses a tree in a pre-order manner.
• In-order Traversal − Traverses a tree in an in-order manner.
• Post-order Traversal − Traverses a tree in a post-order manner.

Node

Define a node having some data, references to its left and right child nodes.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Search Operation

Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Algorithm

struct node* search(int data){
   struct node *current = root;
   printf("Visiting elements: ");
	
   while(current->data != data){
	
      if(current != NULL) {
         printf("%d ",current->data);
			
         //go to left tree
         if(current->data > data){
            current = current->leftChild;
         }//else go to right tree
         else {                
            current = current->rightChild;
         }
			
         //not found
         if(current == NULL){
            return NULL;
         }
      }			
   }
   return current;
}

Insert Operation

Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.

Algorithm

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent = NULL;

      while(1) {                
         parent = current;
			
         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            //insert to the left
				
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }//go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}   

DSA Lab 7: Binary Search Tress

Task:

We have implemented binary search algorithm in previous labs. We we have to implement the binary search tree class "MyBinarySearchTree". Your class should contain all necessary functions in addition to these functions:

• insert(int x);        //it will create new node of integer 'x' and insert new node in the tree
• search(int x);        //it will search integer 'x' in the BST (binary search tree) and return the True or False
• displayPath(int x);        //it will search integer 'x' in the BST (binary search tree) and return the complete path to it from root node this integer

Note: Obviously you have to implement "MyNode" class for BST implementation.

DSA Lab 6: Trees and their traversals

Task:

Implement the class "MyTree" as discussed in class (your tree should be a binary tree - each node have 2 children). For this you have to write a class "MyNode" and create whole tree class using this node class. Your class contains all necessary functions with the additions of these functions:

• display_DFS()        //this will display the whole tree in depth first manner
• display_BFS()        //this will display the whole tree in breath first manner
• MyTress()        //this is the constructor, it will take array of integers and create the whole tree with these integers

DSA Lab 5 - Linked List

Task 1:

Write the complete implementation of double ended queue by using linked list (as discussed in class) containing the following functions:

• enqueueAtTail()
• dequeueAtTail()
• enqueueAtHead()
• dequeueAtHead()
• isEmpty()
• isFull()
• resizeQueue()   // do you really need this function?? think about it!

PS: Best of luck for your mid term lab exam. Don't be late in exams!